- 6.7 Average Value Of A Functional Calculus 14th Edition
- 6.7 Average Value Of A Functional Calculus Equation
5.4 Average Value of a Function. We often need to find the average of a set of numbers, such as an average test grade. Suppose you received the following test scores in your algebra class: 89, 90, 56, 78, 100, and 69. Your semester grade is your average of test scores and you want to know what grade to expect. The average value of a function is just the mean value theorem for integrals. In this lesson, we learn that we can find an area of a rectangle that is exactly the same as the area under the curve. Equating them together and algebraically manipulating the equation will give us the formula for the average value. 8.1 Average Value of a Function on an Interval 8.2 Position, Velocity, and Acceleration Using Integrals 8.3 Using Accumulation Functions and Definite Integrals in Applied Contexts 8.4 Area Between Curves (with respect to x) 8.5 Area Between Curves (with respect to y) 8.6 Area Between Curves - More than Two Intersections.
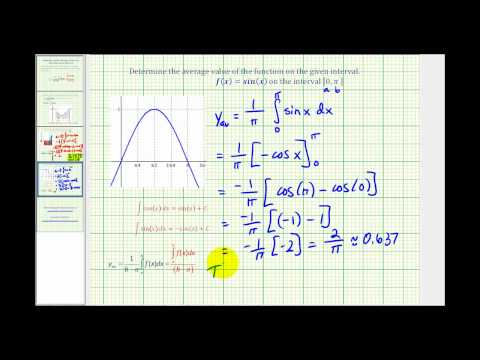
Average Value of a Function. The average height of the graph of a function. For y = f(x) over the domain a, b, the formula for average value is given below. Mean value theorem for integrals. This AP Calculus AB class covers Topic 8.1 - Finding the Average Value of a Function on an Interval, with a tie to Topic 6.7 - The Fundamental Theorem of Calculus and Definite Integrals.
Please provide numbers separated by a comma to calculate the average of the numbers.
What is an average?
6.7 Average Value Of A Functional Calculus 14th Edition
The term average has a number of different meanings. Most generally, it is a single number that is used to represent a collection of numbers. In the context of mathematics, 'average' refers to the mean, specifically, the arithmetic mean. It is a relatively simple statistical concept that is widely used in many areas.
The equation below is one of the more commonly understood definitions of the average:

| Average = |
|
where the sum is the result of adding all of the given numbers, and the count is the number of values being added. For example, given the 5 numbers, 2, 7, 19, 24, and 25, the average can be calculated as such:
6.7 Average Value Of A Functional Calculus Equation
| Average = |
| ||
| = |
| ||
| = | 15.4 |
